EMアルゴリズム

概要

たとえば、複数の信号源があって、そこから毎回確率的にどれかの信号源が選ばれて発生されるデータを観測することを考えます。 ただし観測されたデータは、どの信号源から発生されたかはわからないとします。 また、データにはノイズがのっているなど、各々の信号源も確率的な挙動を示すことにしましょう。

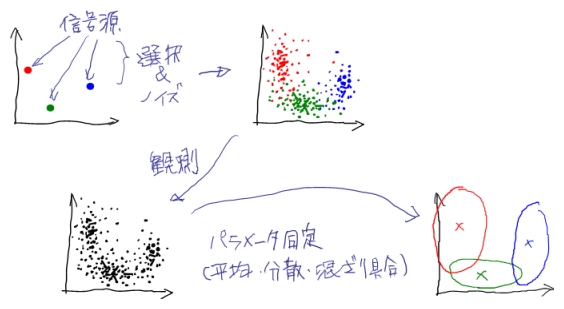
このとき、観測できるデータだけから、確率モデルでモデル化した信号源（と信号源の混ざり具合）のパラメータ同定を行う手法として、以下で説明するEMアルゴリズムを利用することが出来ます。

定義

観測データを \(X\) 、観測できないデータは特に隠れ変数と言い、\(Y\) とします。 どちらも確率変数です。 \(Y\) は上の例で言えば信号源のインデックス（どの信号源が選ばれたか）になります。 観測データと隠れ変数を合わせた \(Z=(X,Y)\) を完全データと言い、システムの全ての確率変数となります。

また便宜上、観測データの定義範囲を \(\Omega_X\)、隠れ変数の定義範囲を \(\Omega_Y\)とします（ \(X\in\Omega_X,Y\in\Omega_Y\) ）。

完全データは、パラメータ \(\theta\) をもつ確率分布によってモデル化しておきます。 すなわち確率密度関数 \(p(X,Y|\theta)\) が分かっているとします。 ここで \(X,Y\) ともに連続的な確率変数として以降も扱いますが、（先の例の \(Y\) のように）離散的な場合でも適宜読み替え（ \(\int\) → \(\sum\) など）を行うだけでOKです。

EM（Expextation Maximization）は、概要の例に限らず一般化すると、ある種の確率密度関数 \(p(X,Y|\theta)\) に対して観測データ \(X\) だけが与えられたときに、 \(\theta\) を効率よく推定することができるアルゴリズムです。 「ある種の」と言いましたが、これは指数型分布族（ガウシアンとか）を指します。

最尤推定

さて、最終的な目標は、観測データ \(X\) を最もよく説明できるパラメータ \(\theta\) を求めることなわけですから、 \(p(X|\theta)\) を \(\theta\) のもっともらしさとして考え、これを最大化すればよいことになります（最尤推定）。 つまり \(\max_\theta \ p(X|\theta)\) 、 あるいは対数尤度の最大化 \(\max_\theta \ \ln p(X|\theta)\) になります。 すると一見あとは \({\partial\over\partial\theta} p(X|\theta)=0\) または \({\partial\over\partial\theta} \ln p(X|\theta)=0\) とすれば（少なくとも極大値は）解析的に求まりそうな気がします。 しかし今は隠れ変数 \(Y\) があるので、尤度は \(p(X,Y|\theta)\) を \(Y\)で積分して周辺化したものになります。

\[p(X|\theta)=\int_{\Omega_Y}p(X,Y|\theta)dY\]

こうなると、極値条件から \(\theta\) を \(X\) だけで書き下すのは難しくなるっぽいので、 反復的に \(\theta_0,\theta_1,\ldots,\theta_t,\ldots\) と徐々に 解に近づけていくことを考えたくなります。

EMアルゴリズムはこの反復計算法を与えます。 しかも！一回の反復につき、尤度が必ず上昇すること（\(p(X|\theta_{t+1}) \ge p(X|\theta_t)\)）が保障されているのです。

対数尤度の分解表現

かなり天下り的ですが対数尤度を変形していきます。

まずベイズの定理により

\[\ln p(X|\theta) = \ln p(X,Y|\theta) - \ln p(Y|X,\theta)\]

です。 次に、確率変数 \(Y\) について任意の確率密度関数を \(q(Y)\) とします。 確率分布なので

\[\int_{\Omega_Y} q(Y)dY=1\]

なのと、 \(\ln p(X|\theta)\) は \(Y\) に関係ないことから、

\[\ln p(X|\theta) = \ln p(X|\theta) \int_{\Omega_Y} q(Y) dY = \int_{\Omega_Y} q(Y) \ln p(X|\theta) dY\]

とできます。 一方で

\[\ln p(X|\theta) = \ln p(X,Y|\theta) - \ln q(Y) + \ln q(Y) - \ln p(Y|X,\theta) = \ln{p(X,Y|\theta) \over q(Y)} + \ln{q(Y) \over p(Y|X,\theta)}\]

なので、合わせて

\[\ln p(X|\theta) = \int_{\Omega_Y} q(Y) \ln{p(X,Y|\theta) \over q(Y)} dY + \int_{\Omega_Y} q(Y) \ln{q(Y) \over p(Y|X,\theta)} dY\]

と導くことができます。 第2項は \(q(Y)\) から \(p(Y|X,\theta)\) の（確率変数 \(Y\) についての）カルバック・ライブラー情報量として知られているものになっています。 これを \(KL(q \parallel p_{|X,\theta})\) と書くことにします。

EMアルゴリズム

これでやっとEMアルゴリズムを説明できるところまで来ました。

EMはEステップとMステップという2段階から成っています。 ステップと言ってますが、これはあくまで数学的な導出のステップであって、 計算機で実現する意味でのステップとは違います。

ではパラメータを \(\theta^t\) から \(\theta^{t+1}\) に更新することを考えます。 以下、

• \(X, \theta^t, \theta^{t+1}\) は、実際にはデータとしての値が入るもの
• \(Y, \theta\) は、数学的な意味での変数

であることを念頭に置くと理解しやすいかもしれません。

Expectation Step

先の対数尤度の分解表現において、\(q(Y)\) は正規化されていればなんでもよかったので、\(q(Y) = p(Y \mid X,\theta^t)\) とします。

\[\ln p(X|\theta) = \int_{\Omega_Y} p(Y|X,\theta^t) \ln{p(X,Y|\theta) \over p(Y|X,\theta^t)} dY + KL(p_{|X,\theta^t} \parallel p_{|X,\theta})\]

第1項を \(L(\theta, \theta^t)\) と置きます。 また、

\[L(\theta, \theta^t) = \int_{\Omega_Y} p(Y|X,\theta^t) \ln p(X,Y|\theta) dY - \int_{\Omega_Y} p(Y|X,\theta^t) \ln p(Y|X,\theta^t) dY\]

で、第1項を

\[Q(\theta, \theta^t) = \int_{\Omega_Y} p(Y|X,\theta^t) \ln p(X,Y|\theta) dY\]

と置きます。

Eステップはこの \(Q(\theta, \theta^t)\) の導出ということになります。 \(Q(\theta, \theta^t)\) は、完全データの対数尤度 \(\ln p(X,Y|\theta)\) を確率分布 \(p(Y|X,\theta^t)\) で期待値計算したものといえます。

Maximization Step

Mステップではその名の通り、

\[L(\theta, \theta^t) = Q(\theta, \theta^t) - \int_{\Omega_Y} p(Y|X,\theta^t) \ln p(Y|X,\theta^t) dY\]

を \(\theta\) について最大化して、そのときの \(\theta\) を \(\theta_{t+1}\) とします。 ここで \(L(\theta, \theta^t)=\cdots\) の第2項は \(\theta\) に関係ないので、結局

\[\theta^{t+1} = \arg\max_\theta Q(\theta, \theta^t)\]

と等価です。

最大化は結局（多くの場合） \({\partial\over\partial\theta}Q=0\) とやるわけで、\(Q\) の極値を解析的に求めるのって無理そうじゃん・・・って思われますがそうでもありません。 \(Q\) の定義を良く見ると、\(\theta\) に関係あるのは \(\ln p(X,Y|\theta)\) だけです。 \(p(X,Y|\theta)\) がガウシアンとかなら （冒頭の \({\partial\over\partial\theta} \ln p(X|\theta)=0\) に比べれば） かなり簡単になりそうな予感がします。 実際のところは適用例を見てみてください。

あとはEステップ・Mステップを収束するまで繰り返せばいいわけですね。 そして \(\theta\) が決まれば、たとえば \(p(Y|X,\theta)=p(X,Y|\theta)/p(X|\theta)\) が計算できるので、任意の \(X\) に対する \(Y\) の推定ができたりします。 最初の例でいえば、新たな観測データに対する発生源の判別、つまりクラスタリングができます。 他にも回帰とかにも使えそうです。

対数尤度の単調増加

パラメータ \(\theta_t\) での対数尤度は、同一の確率分布どうしのカルバック・ライブラー情報量はゼロになるので、

\[\begin{array}{ll} \ln p(X|\theta^t) &= L(\theta^t, \theta^t) + KL(p_{|X,\theta^t} \parallel p_{|X,\theta^t}) \\ &= L(\theta^t, \theta^t) \end{array}\]

となります。 一方パラメータ \(\theta_{t+1}\) での対数尤度は

\[\ln p(X|\theta^{t+1}) = L(\theta^{t+1}, \theta^t) + KL(p_{|X,\theta^t} \parallel p_{|X,\theta^{t+1}})\]

となります。

Mステップの定義から明らかに

\[L(\theta^{t+1}, \theta^t) \ge L(\theta^t, \theta^t)\]

で、異なる確率分布間のカルバック・ライブラー情報量は正ですから、

\[\ln p(X|\theta^{t+1}) \ge \ln p(X|\theta^t)\]

が必ず成立します。

適用例

• Gaussian Mixture Model
• Hidden Markov Model