SVD

特異値分解(Singular Value Decomposition)は、任意の \(m\times n\) 行列 \(G\) を \(G = U \Sigma V^*\) の形に分解します。 なお以下では、実数を成分とする行列のみ扱い、\(G = U \Sigma V^T\) とします。

もし \(G\) が正則行列（したがって正方行列）の場合は、

• \(\Sigma\) ：対角成分が特異値の対角行列
• \(U,\,V\) ：直交行列

となり、逆行列が \(G^{-1} = V \Sigma^{-1} U^T\) のように求まります。

\(G\) が非正則または非正方な場合でも、\(\Sigma,\,U,\,V\) は似たような性質を持ち、 \(G^{+} = V \Sigma^{+} U^T\) で擬似逆行列を計算することができます。 （\(\Sigma^{+}\) は \(\Sigma^T\) で非ゼロの特異値を逆数にしたもの）

擬似逆行列 for 線形連立方程式

擬似逆行列が求まるので、線形連立方程式を汎用的に解くことができます。 ふつうの線形連立方程式の場合はその解が、優決定(over-determined)な場合は最小二乗解が、 劣決定(under-determined)な場合はノルム最小解が求まります。

主双対内点法 のアルゴリズムでも、 線形連立方程式の解を求める必要があります。 主双対内点法の場合は正方行列であり、 対象の最適化問題によっては必ず正則になることもあるので、 SVDだとオーバースペックかもしれません。 しかし、問題によっては求解途中に特異的になったり、 （\(A\) などの）係数パラメータが実データから決まるせいで ゼロがちになったりすることもありうるかと思います。 こういうときでも安定して使えるのでやはりSVDが便利です。

One-sided Jacobi for SVD

SVDにもいろいろなアルゴリズムがあるようですが、 LAPACK Working Notes lawn15の Algorithm 4.1にあるOne-sided Jacobi for SVDがいちばんシンプルでわかりやすそうです。 ただlawn15では簡単のため正方行列を前提にしているようです。 ここでは非正方行列も考慮します。

非正方行列の考慮にあたり、 \(U,\,\Sigma,\,V\) の形状などはいろいろなパターンが考えられるようですが、ここでは

• \(m \ge n\)（\(m \lt n\) の場合は\(G^T\)を分解すればよい）を前提にして、
  • \(U\) ： \(m \times n\)
  • \(\Sigma\) ： \(n \times n\)、特異値のならび（昇順・降順）は特に問わない
  • \(V\) ： \(n \times n\)

とします。

アルゴリズム

• パラメータ
  • \(\tau\)：計算機イプシロン程度の値
• 初期化
  • \(U \leftarrow G\)　
  • \(V \leftarrow I\)　
• 以下を繰り返し
  • \(1 \le i \lt j \le n\) のすべての \(i,\,j\) について
    • \(u_i\) を \(U\) の \(i\) 列目の列ベクトルとする（\(u_j,\,v_i,\,v_j\) も同様に定義）
    • \(a = u_i^T u_i,\,b = u_j^T u_j,\,d = u_i^T u_j\) を算出
    • 収束条件 \(d^2 \le \tau^2 a b\) を満たしていなかったら以下を計算
      • \(\zeta = {b - a \over 2d}\)　
      • \(t = {sign(\zeta) \over \mid\zeta\mid + \sqrt{1 + \zeta^2}}\)　
      • \(c = {1 \over \sqrt{1 + t^2}},\,s = ct,\, R = \left[ \begin{array}{cc} c & s \\ -s & c \end{array} \right]\)　
      • \([u_i \quad u_j] \leftarrow [u_i \quad u_j] R\)　
      • \([v_i \quad v_j] \leftarrow [v_i \quad v_j] R\)　
  • すべての \(i,\,j\) の収束条件が満たされていたら繰り返しを出る
• 正規化と特異値の算出
  • 特異値 \(\sigma_i = \|u_i\| \qquad(1 \le i \le n)\)
  • 特異値をベクトル \(\sigma\) として \(\Sigma = {\bf diag}(\sigma)\)　
  • \(u_i \leftarrow {u_i \over \|u_i\|} \qquad(1 \le i \le n)\)　

解釈

繰り返しの内側部分は、\(n\) 列から2列選ぶ \({}_nC_2\) 通り分のループになっています。 ループ中、\(U,\,V\) （の各々2列）が逐次更新されていきますが、 この更新では \(UV^T=G\) の関係が常に保たれます。 というのも、この更新は（\(2 \times 2\) 回転行列 \(R\) による演算と等価な）\(n \times n\) 直交行列 \(R'\) を用いて、

\[UV^T \rightarrow (UR')(VR')^T = UR'R'^TV^T = UV^T = G\]

のように書けるためです。

そして \(R'\) すなわち \(R\) の成分 \(c,s\) は、 \((UV^T)^T UV^T = VU^T UV^T\) を考えた時の \(U^TU\) の \((i,j)\) 要素 （\(U^TU\)は対象行列なので \((j,i)\) 要素も）をゼロにするような値に計算されています。

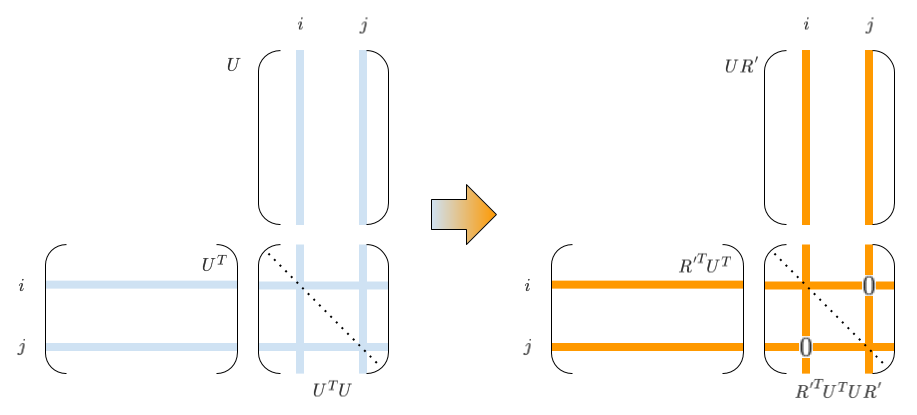
したがって、収束して繰り返しを出たときには、\(U^TU\) は（\(\tau\) で許容されるレベルで） 対角行列になっているので、\(U\) の各列正規化で \(U \rightarrow U {\bf diag}(\sigma)\) のように分離して、 互いに異なる列が直交する \(U\) と、対角行列 \(\Sigma\) を得ることができます。 \(V\) も、単位行列に直交行列をどんどんかけていったものなので、 直交行列になっていることがわかります。

実装例

SVDマルチスレッド実装 参照。