SOCP Class Reference

A Second-Order Cone Program solver class. More...

#include <SOCP.h>

Inheritance diagram for SOCP:

Public Member Functions
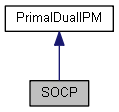
IPM_Error	solve (IPM_Vector &x, const IPM_Vector &f, const IPM_Matrix G[], const IPM_Vector h[], const IPM_Vector c[], const IPM_Single d[], const IPM_uint m, const IPM_Matrix &A, const IPM_Vector &b)
	Runs the solver with given parameters. More...
bool	isConverged (void)
	Indicates if the previous solve() has converged or not.
Public Member Functions inherited from PrimalDualIPM
	PrimalDualIPM ()
	Constructor.
virtual	~PrimalDualIPM ()
	Destructor.
void	setLog (std::ostream *pOuts)
	Sets output destination of internal calculation log. More...

Protected Attributes
IPM_Scalar	m_eps_bd
	Value of \( \epsilon_{\rm bd} \).
IPM_Scalar	m_slack
	Initial margin value for an auxiliary variable.
Protected Attributes inherited from PrimalDualIPM
IPM_Scalar	m_margin
	Initial margin value for dual variables of inequalities.
IPM_Scalar	m_loop
	Max iteration number of outer-loop for the Newton step.
IPM_Scalar	m_bloop
	Max iteration number of inner-loop for the backtracking line search.
IPM_Scalar	m_eps_feas
	Tolerance of the primal and dual residuals.
IPM_Scalar	m_eps
	Tolerance of the surrogate duality gap.
IPM_Scalar	m_mu
	The factor to squeeze complementary slackness.
IPM_Scalar	m_alpha
	The factor to decrease residuals in the backtracking line search.
IPM_Scalar	m_beta
	The factor to decrease a step size in the backtracking line search.
IPM_Scalar	m_s_coef
	The factor to determine an initial step size in the backtracking line search.

Additional Inherited Members
Protected Member Functions inherited from PrimalDualIPM
void	logWarn (const char *str)
	Logs a warning message. More...
void	logVector (const char *str, IPM_Vector_IN v)
	Logs values of a vector, transposing if it is a colomn vector. More...
void	logMatrix (const char *str, IPM_Matrix_IN m)
	Logs values of a matrix. More...
IPM_Error	start (const IPM_uint n, const IPM_uint m, const IPM_uint p)
	Starts to solve a optimization problem by primal-dual interior-point method. More...
Static Protected Member Functions inherited from PrimalDualIPM
static IPM_Scalar	max (const IPM_Scalar a, const IPM_Scalar b)
	Returns the larger of a and b.
static IPM_Scalar	min (const IPM_Scalar a, const IPM_Scalar b)
	Returns the smaller of a and b.
static IPM_Scalar	abs (const IPM_Scalar x)
	Returns the absolute value of x.

Detailed Description

A Second-Order Cone Program solver class.

The problem is \[ \begin{array}{ll} {\rm minimize} & f^T x \\ {\rm subject \ to} & \| G_i x + h_i \|_2 \le c_i^T x + d_i \quad (i = 0, \ldots, m - 1) \\ & A x = b, \end{array} \] where

• variables \( x \in {\bf R}^n \)
• \( f \in {\bf R}^n \)
• \( G_i \in {\bf R}^{n_i \times n} \), \( h_i \in {\bf R}^{n_i} \), \( c_i \in {\bf R}^n \), \( d_i \in {\bf R} \)
• \( A \in {\bf R}^{p \times n} \), \( b \in {\bf R}^p \).

Internally an approximately equivalent problem is formed and an auxiliary variable \( s \in {\bf R}^m \) is introduced for the infeasible start method as follows: \[ \begin{array}{lll} {\rm minimize}_{x,s} & f^T x \\ {\rm subject \ to} & {\| G_i x + h_i \|_2^2 \over s_i} \le s_i & (i = 0, \ldots, m - 1) \\ & s_i \ge \epsilon_{\rm bd} & (i = 0, \ldots, m - 1) \\ & c_i^T x + d_i = s_i & (i = 0, \ldots, m - 1) \\ & A x = b, \end{array} \] where \( \epsilon_{\rm bd} > 0 \) indicates the extent of approximation that excludes \( c_i^T x + d_i = 0 \) boundary.

Member Function Documentation

IPM_Error SOCP::solve	(	IPM_Vector &	x,
		const IPM_Vector &	f,
		const IPM_Matrix	G[],
		const IPM_Vector	h[],
		const IPM_Vector	c[],
		const IPM_Single	d[],
		const IPM_uint	m,
		const IPM_Matrix &	A,
		const IPM_Vector &	b
	)

Runs the solver with given parameters.

Parameters

x	[IN-OUT] is a column vector containing values of \(x\). It is used as the initial values and overwritten with the final results.
f	[IN] is a column vector containing values of \(f\).
G	[IN] is an array of matrices containing values of \(G_0, \ldots, G_{m-1}\).
h	[IN] is an array of vectors containing values of \(h_0, \ldots, h_{m-1}\).
c	[IN] is an array of vectors containing values of \(c_0, \ldots, c_{m-1}\).
d	[IN] is an array of single element matrices containing values of \(d_0, \ldots, d_{m-1}\).
m	is \(m\), the number of inequality constraints.
A	[IN] is a matrix containing values of \(A\).
b	[IN] is a vector containing values of \(b\).

Here is the call graph for this function:

---

The documentation for this class was generated from the following files:

• SOCP.h
• SOCP.cpp